2.23. Funções

Uma forma de modularizar programas consiste em organizá-los em procedimentos ou funções. Uma função é um bloco de código auto-contido, identificado com um nome, uma lista de parâmetros e que pode ser invocada em nossos programas da mesma forma que as funções da linguagem Python.

A Figura 2.21 apresenta a lógica de uso de uma função denominada f. Repare que o programa após executar os comandos comando #1 e comando #2, desvia seu fluxo de execução ao atingir o comando v = f(...). Nesse ponto dizemos que a função f foi chamada ou invocada. O fluxo é então desviado para a sequência de instruções definida pela função, mostrada no lado direito da Figura 2.21. A sequência de comandos da função f é encerrada quando o comando return é encontrado, devolvendo o controle do programa para a linha onde a função foi chamada. O valor produzido pela função f será associado ao nome v (ou variável v) e o programa continuará a execução da sequência de instruções a partir do comando comando #i + 1.

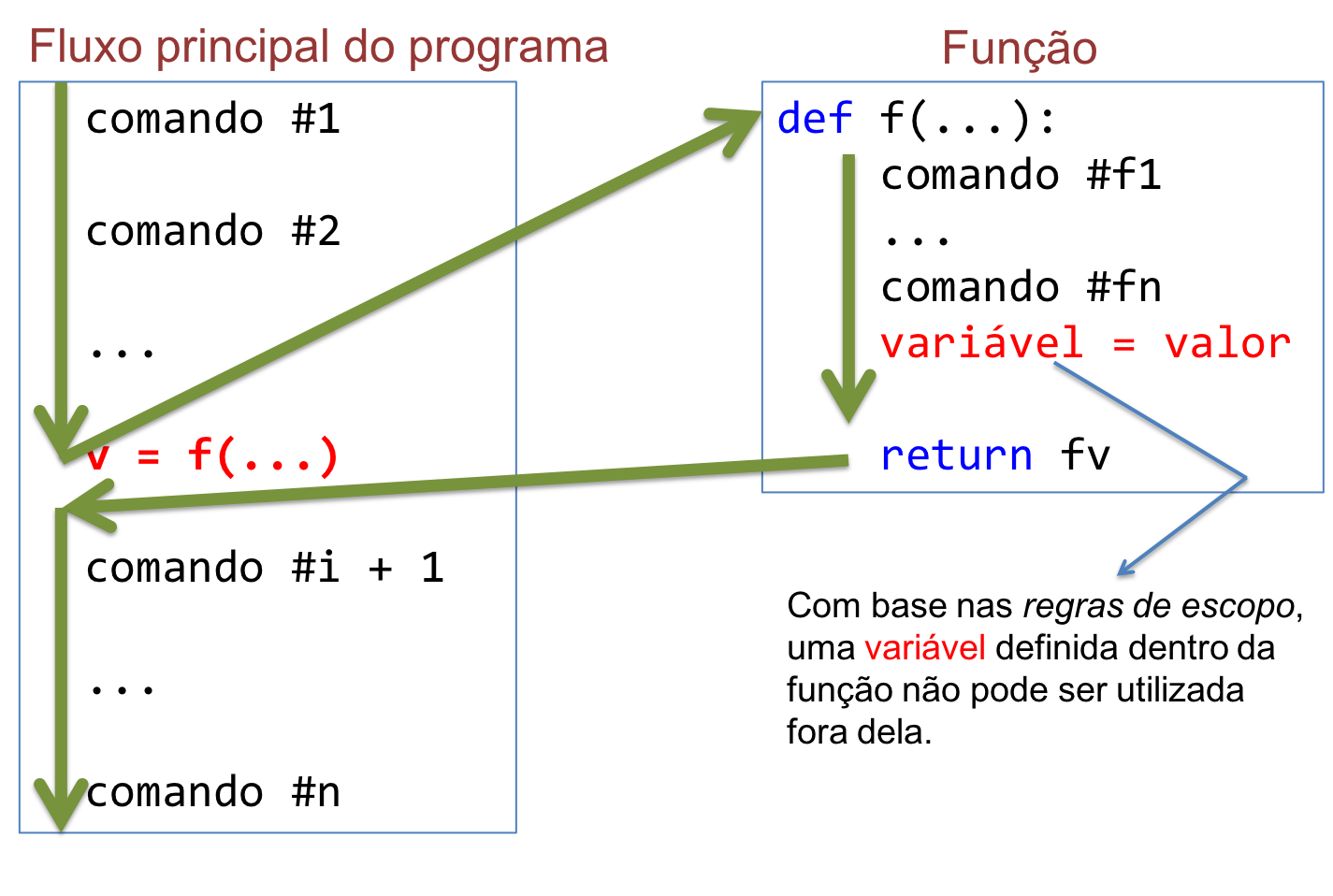
Figura 2.21 - Ilustração do processo de chamada de uma função.

Vamos supor um programa hipotético com a sequência de comandos mostrada na parte esquerda da Figura 2.22. Suponha também que esse programa tenha que realizar o cálculo da distância euclidiana entre dois pontos em algumas seções do código. Nesse caso, teríamos um programa com várias seções de código muito semelhantes, com, possivelmente, pequenas variações, como diferentes pares de pontos para computar a distância. Agora, pense em seções de código que realizem computações mais complexas, tais como cálculo de derivadas e integrais, ordenação de conjuntos de elementos e outras computações que exigem muitos passos para serem expressas. Nesse caso, teríamos programas muito grandes e extremamente difíceis de dar manutenção. Novamente, suponha que você descubra um erro em uma dessas seções muito parecidas e que este erro seja comum a todas as seções. Você deveria varrer todo o seu código e corrigir esse erro em todas as seções pois, caso uma delas fique sem a aplicação dessa correção, seu programa possivelmente apresentará bugs ou produzirá resultados indesejados.

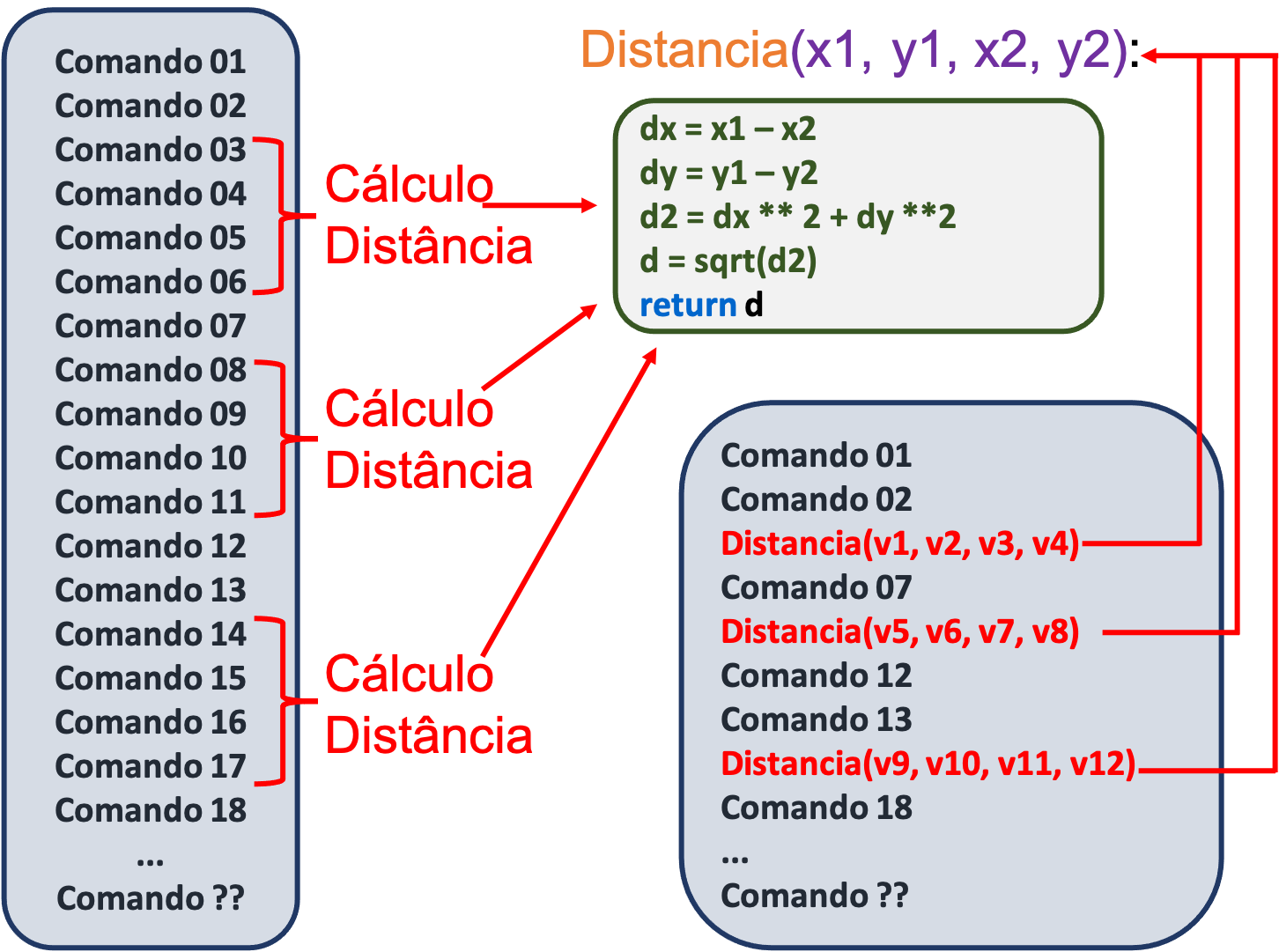
Figura 2.22 - Encapsulando seções de códigos comuns na forma de funções.

A abstração de códigos na forma de funções é uma das maneiras criadas para evitar esse tipo de problema. Suponha que as seções comuns na parte esquerda da Figura 2.22 sejam encapsuladas na forma de um código mais geral e reutilizável no programa através de uma função denominada Distancia. Neste caso, o programa do lado esquerdo na Figura 2.22 seria reduzido à sequência de comandos mostrada na parte inferior direita dessa mesma figura. Repare que agora, temos uma seção comum que captura a computação da distância euclidiana, que será usada nas linhas destacadas em vermelho do programa. Dessa forma, qualquer alteração no código da função irá refletir automaticamente nas linhas que realizam sua chamada.

2.23.1. Definindo uma Função

Uma função em Python pode ser definida utilizando a palavra reservada def seguida do nome da função e a lista de parâmetros formais dessa função. A Figura 2.23 mostra a definição da função Fatorial. A linha com a assinatura ou declaração da função é terminada com o símbolo :. Logo abaixo dessa linha, incluímos o corpo da função, isto é, uma sequência de comandos que implementa a funcionalidade a ser fornecida pela função. Repare que a sequência de comandos do corpo da função deve ser indentada, isto é, a sequência deve possuir um recuo à direita. Em geral, usamos 04 espaços nesse recuo.

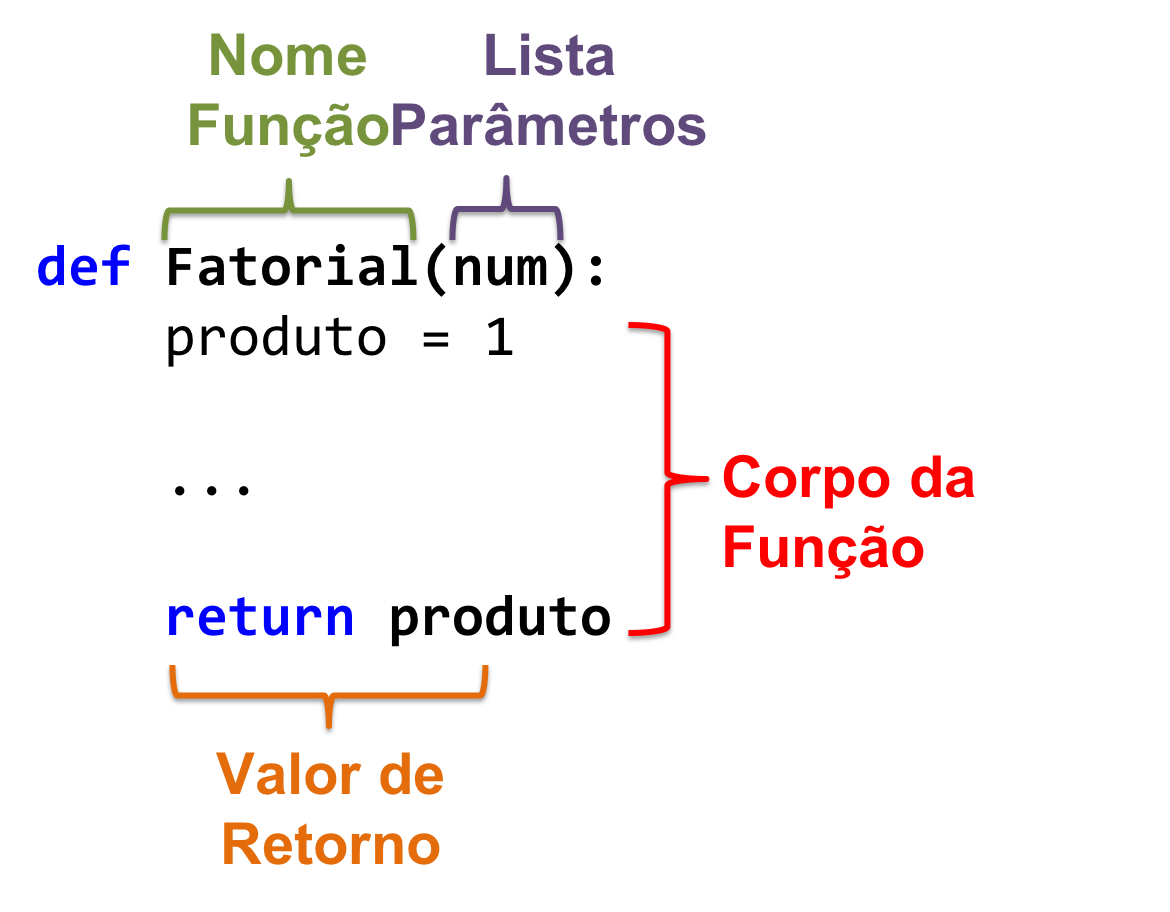
Figura 2.23 - Definição de uma função chamada Fatorial.

A instrução return pode ser usada para indicar um ponto de saída da função, isto é, um ponto em que ela já tenha realizado sua computação e deva retornar um ou mais valores produzidos pela função.

Nota

Uma função pode não retornar nenhum valor, como é o caso da função print de Python que apenas escreve um texto na saída padrão. Nesse tipo de função a instrução return pode ser utilizada sem nenhuma expressão a sua direita.

Nota

Em Python uma função pode retornar mais de um valor. Nesse caso a instrução return pode ser usada para retornar uma lista de valores.

A função Fatorial, mostrada no Trecho de Código 2.17, computa o fatorial de um número inteiro positivo:

Trecho de Código 2.17 - Função para cálculo do fatorial (versão iterativa).

def Fatorial(num):

    if (num < 0) or (type(num) != int):
        raise ValueError("O Fatorial só é definido para números inteiros positivos!")

    produto = 1

    while(num > 0):
        produto = produto * num

        num = num - 1

    return produto

Repare na definição da função Fatorial (linha 01) que ela possui um único parâmetro formal chamado num. Isso indica que a função Fatorial deverá ser chamada com apenas um argumento. Além disso, na linha 13 após terminar a computação do valor do fatorial, que estará associado ao nome produto, a instrução return irá retornar o fluxo de execução do programa para a linha do programa que tiver chamado essa função, devolvendo o valor associado a essa variável (produto).

Na definição da função Fatorial acima, ainda podemos observar que o bloco de comandos contido na função encontra-se indentado com 04 espaços. A linha 04 possui um recuo maior pois esse comando faz parte do comando if da linha 03. Da mesma maneira, as linhas 9 e 11 possuem um recuo maior pois fazem parte da instrução while da linha 08.

O trecho de código abaixo mostra como essa função pode ser chamada em um programa, supondo que ela tenha sido definida anteriormente:

print("Exemplo de uso da função Fatorial!")

resultado = Fatorial(6)

print(resultado)

Na linha 03 do programa acima, ao chamar a função Fatorial com o valor 6 como argumento dessa função, o fluxo de controle é passado para a sequência de comandos do corpo da função Fatorial. O valor 6 será associado ao parâmetro num na função Fatorial, ou seja, dentro da função esse valor 6 será usado através da variável num. A linha 13 da função Fatorial (Trecho de Código 2.17) retorna o valor calculado, que ficará então associado ao nome resultado na linha 3 do programa, que então voltará a executar sua sequência de instruções.

Agora, vamos criar uma nova função para calcular a distância euclidiana entre dois pontos no espaço cartesiano (Trecho de Código 2.18):

Trecho de Código 2.18 - Função para cálculo da distância euclidiana entre dois pontos.

import math

def DistanciaEuclidiana(x1, y1, x2, y2):

    dx = x1 - x2
    dy = y1 - y2

    d = math.sqrt(dx**2 + dy**2)

    return d

Essa nova função foi nomeada de DistanciaEuclidiana, sendo definida com quatro parâmetros: x1, y1, x2, e y2. Portanto, para ser usada em um programa ela deverá ser chamada fornecendo quatro argumentos, como no programa abaixo:

d1 = DistanciaEuclidiana(0, 0, 1, 1)

print(d1)

d2 = DistanciaEuclidiana(2, 3, 10, 3)

print(d2)

Se você informar um número menor de argumentos na chamada da função DistanciaEuclidiana, como no trecho de código abaixo, o interpretador Python irá lançar uma exceção, indicando o erro da falta do quarto parâmetro:

d3 = DistanciaEuclidiana(0, 0, 1)

Saída:

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
TypeError: DistanciaEuclidiana() missing 1 required positional argument: 'y2'

Nota

A definição de uma função não faz com que o corpo da função seja executada. O corpo somente é executado quando a função é chamada (ou invocada). Mas repare que para chamarmos uma função, primeiro ela deve ter sido definida em alguma parte de nosso programa.

Nota

A definição de uma função é um comando Python.

2.23.2. Funções Recursivas

Como pode ser visto na função DistanciaEuclidiana (Trecho de Código 2.18), uma função pode chamar outras funções, como foi o caso da função math.sqrt da biblioteca padrão de Python, chamada na linha 08. Isso possbilita a construção de programas bem organizados, agrupando a lógica em várias funções menores, cada uma com um papel bem definido.

Outro recurso das linguagens de programação é a criação de funções recursivas, isto é, funções que são definidas através de chamadas à própria função. Esse recurso é muito importante pois vários problemas são inerentemente recursivos por natureza. Por exemplo, o fatorial de um número \(n\), com \(n \in Z^+\), pode ser definido através da seguinte equação de recorrência:

(2.4)\[\begin{split}\begin{cases} fat(1) = 1, & \text{se $n = 1$}\\ fat(n) = n \times fat(n - 1), & \text{se $n > 1$} \end{cases}\end{split}\]

Uma função para calcular o fatorial poderia ser expressa da seguinte forma (Trecho de Código 2.19):

Trecho de Código 2.19 - Função para cálculo do fatorial (versão recursiva).

def FatorialRec(n):

    if n == 1:
        return 1
    else:
        return n * FatorialRec(n - 1)

Repare no Trecho de Código 2.19, como essa versão da função fatorial é mais simples de ser compreendida do que a função definida no início dessa aula, que foi construída de forma iterativa através de um laço do tipo while (Trecho de Código 2.17).

A forma de usar a função FatorialRec é a mesma de uma função não-recursiva:

print("Exemplo de uso da função fatorial recursiva!")

resultado = FatorialRec(6)

print(resultado)

Nota

Nem sempre um algoritmo implementado de forma recursiva será mais fácil de ser compreendido do que sua versão iterativa.

Nota

Muitas vezes, as funções recursivas podem sofrer com problemas de eficiência, uma vez que elas fazem com que as chamadas sejam empilhadas diversas vezes. Mas uma boa prática de programação consiste em primeiro construir um algoritmo que funcione corretamente e depois otimizá-lo, seja removendo a recursividade ou utilizando alguma técnica especial.

Nota

Vários compiladores eliminam automaticamente a recursividade durante a compilação de uma função recursiva. No entanto, Python não faz isso.

Um exemplo de mau emprego da recursividade ocorre no cálculo de um termo da sequência de Fibonacci. Lembrando que essa sequência é definida através da seguinte fórmula de recorrência:

(2.5)\[\begin{split}\begin{cases} F_1 = 1 \\ F_2 = 1 \\ F_n = F_{n-1} + F_{n-2} \end{cases}\end{split}\]

Portanto, essa fórmula nos permitiria computar os termos da série:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

Vamos criar uma função chamada FibRec que implemente essa fórmula de maneira recursiva (Trecho de Código 2.20):

Trecho de Código 2.20 - Função para cálculo da sequência de Fibonacci (versão recursiva).

def FibRec(n):
    if (n == 1) or (n == 2):
        return 1
    else:
        return FibRec(n - 1) + FibRec(n - 2)

Para calcularmos o nono termo da série, poderíamos chamar a função FibRec da seguinte maneira:

FibRec(9)

A versão iterativa da função que computa os termos de Fibonacci é mostrada abaixo (Trecho de Código 2.21):

Trecho de Código 2.21 - Função para cálculo da sequência de Fibonacci (versão iterativa).

def FibIter(n):
    a, b = 1, 1

    while n > 2:
        a, b = b, a + b
        n -= 1

    return b

Assim como na função recursiva, nessa versão iterativa para calcularmos o nono termo da série basta chamar a função FibIter:

FibIter(9)

Questão: Qual a diferença na forma de computar os termos da série de Fibonacci entre as versões recursiva (FibRec) e iterativa (FibIter)?

Solução: Repare que enquanto a versão iterativa reaproveita os valores calculados em cada iteração, a versão recursiva recomputa todos os valores já computados em alguma outra chamada recursiva.

Nota

Veja que essa diferença não ocorre entre as versões recursiva e iterativa da função fatorial, pois o fatorial recursivo nunca chama novamente a função fatorial para um mesmo número.

2.23.3. Funções com Número Variável de Argumentos

Em geral, as linguagens de programação imperativa permitem criar funções que podem ser chamadas com um número diferente de argumentos. Em Python temos três formas de construir funções com número variável de argumentos. Esta seção discute como criar tais funções.

2.23.3.1. Parâmetros Default

Os parâmetros de uma função podem ser associados a valores default, isto é, caso o parâmetro seja omitido na chamada da função, o valor default será utilizado. Dessa forma, podemos criar uma função que pode ser chamada com um número menor de argumentos do que a lista de parâmetros da sua definição.

A função Graus2Radianos mostrada abaixo define o valor padrão de 3.14 para o parâmetro pi:

def Graus2Radianos(alpha, pi=3.14):
    x = alpha * pi / 180.0

    return x

A função acima pode ser chamada com apenas um argumento, onde informamos o valor do ângulo alpha a ser convertido de graus para radianos:

Graus2Radianos(45)

Ou pode ser chamada informando-se um novo valor para o parâmetro pi:

Graus2Radianos(45, 3.1)

Como pode ser visto, ao definirmos um parâmetro como tendo um valor default, tornamos esse parâmetro opcional.

Nota

É importante notar que os valores de parâmetros default são avaliados da esquerda para a direita quando a função é definida. Além disso, esses valores são definidos uma única vez no programa, exatamente no ponto de definição da função.

Nota

Outro ponto importante é que após a definição de um parâmetro opcional, os demais parâmetros também devem ser opcionais, caso contrário será gerado um erro na compilação do código:

SyntaxError: non-default argument follows default argument

2.23.3.2. Chamando Funções com Argumentos Nomeados

Uma função também pode ser chamada com os argumentos na forma de pares nome/valor (keyword arguments):

Graus2Radianos(pi=3.1, alpha=45)

Graus2Radianos(alpha=45)

Essa facilidade faz com que não precisemos lembrar a ordem exata dos argumentos em sua chamada.

2.23.3.3. Parâmetros *args e **kwargs

Em Python, podemos utilizar os parâmetros especiais *args e **kwargs para definir funções com um número variável de argumentos. A primeira forma, *args (com um único *), permite criar uma função que aceite uma sequência de parâmetros não nomeados de qualquer tamanho. A função MyPrintV1, mostrada abaixo, utiliza esse tipo de parâmetro para imprimir os valores informados como argumentos:

def MyPrintV1(*args):
    for a in args:
        print(a)

Podemos chamar a função acima com um único argumento do tipo string:

MyPrintV1("p1")

Ou, com diversos números inteiros:

MyPrintV1(1, 3, 5, 7, 9)

Ou, com números em ponto flutuante e uma string:

MyPrintV1(-20.38, -43.50, "Ouro Preto")

Nota

O parâmetro *args é na verdade uma tupla do Python.

A segunda forma de criar uma função que aceita um número variável de argumentos é usar o tipo **kwargs (com um duplo *). Esse tipo de parâmetro pode ser usado para definir uma função que aceite uma lista de parâmetros nomeados de qualquer tamanho. Esse conjunto variável de parâmetros é representado como um dicionário. A função MyPrintV2, mostrada abaixo, utiliza esse tipo de parâmetro para imprimir os nomes e os valores dos argumentos informados na sua chamada:

def MyPrintV2(**kwargs):
    for k, v in kwargs.items():
        print( "parametro: {}, valor:{}".format(k, v) )

A chamada abaixo passa três argumentos:

MyPrintV2(latitude=-20.38, longitude=-43.50, nome="Ouro Preto")

A chamada abaixo realiza a chamada da função MyPrintV2 com dois argumentos:

MyPrintV2(longitude=-45.88, latitude=-23.17)

2.23.4. Unpacking Argument Lists

Um situação muito comum é termos a lista de argumentos que desejamos passar a uma função em uma sequência (lista ou tupla) ou como membros de um dicionário e a função estar definida como parâmetros separados, como a função Graus2Radianos definida anteriormente. Nesse caso, podemos usar um artifício prático da linguagem Python para transformar esse objetos na sequência correta a ser informada na chamada da função. O exemplo abaixo mostra como podemos transformar os elementos de uma lista l no único valor a ser informado na chamada da função Graus2Radianos:

l = [45]

Graus2Radianos(*l)

O próximo exemplo mostra como podemos transformar a lista l contendo os dois argumentos que desejamos utilizar na chamada da função Graus2Radianos:

l = [45, 3.1]

Graus2Radianos(*l)

Finalmente, o exemplo abaixo mostra como podemos utilizar os pares chave/valor de um dicionário como argumentos nomeados na chamada da função Graus2Radianos:

d = {
    "pi": 3,
    "alpha": 45
}

Graus2Radianos(**d)

2.23.5. Expressões Lambda

Uma Expressão Lambda é uma pequena função anônima criada com a palavra chave lambda, que permite introduzir uma função definida por uma única expressão sem a necessidade de associar um nome. As expressões lambda são muito utilizadas em Python, podendo ser usadas em qualquer lugar que é preciso informar alguma função.

Exemplo:

>>> pairs = [(1, 'one'), (2, 'two'), (3, 'three'), (4, 'four')]

>>> pairs.sort(key=lambda pair: pair[1])
>>> pairs

ou:

>>> pairs.sort(key=lambda pair: pair[0])
>>> pairs

Exemplo:

>>> l = [ 1, 2, 3, 4, 5 ]

>>> pot = map(lambda x: x**2, l)
>>> pot

>>> list(pot)

Exemplo:

>>> u = [ 1, 2, 3, 4, 5 ]
>>> v = [ 10, 11, 12, 13, 14 ]

>>> soma = map(lambda x, y: x + y, u, v)

>>> list(soma)

Exemplo:

>>> pares = filter(lambda x: x % 2 == 0, u)
>>> list(pares)